
- #PSEUDO RANDOM NUMBER GENERATOR ALGORITHM MATHEMATICA GENERATOR#
- #PSEUDO RANDOM NUMBER GENERATOR ALGORITHM MATHEMATICA SERIES#
John von Neumann himself joked about it: "Anyone who considers arithmetical methods of producing random digits is, of course, in a state of sin. The irregularity of the grid shows that the procedure succeeds in producing a random-looking output in spite of the simplicity and deterministic nature of the procedure. One way to avoid this is to pad with 1s rather than 0s, as was done in this Demonstration.Įach iteration starts from a random seed and produces a sequence of sequences of numbers generating the grid shown. In other words, the method eventually reaches a fixed point. Another flaw is when the sequence reaches 000…, from which all squares from then on are 0 and the resulting sequences (after padding) are also 0. Of course there are at most only different numbers, so eventually the whole sequence repeats in the same order and eventually a number comes up that was squared before. use that number as the seed for the next iteration take the middle digits of the resulting number as the "random number"Ĥ.
#PSEUDO RANDOM NUMBER GENERATOR ALGORITHM MATHEMATICA SERIES#
Iterating von Neumann's procedure produces a series of numbers generated by a deterministic process intended merely to imitate a random sequence. John von Neumann suggested it in 1946 for the purpose of devising, together with Stan Ulam, what would later become known as the Monte Carlo method for the simulation of physical processes, motivated by their work at Los Alamos National laboratory while building the atomic bomb.
#PSEUDO RANDOM NUMBER GENERATOR ALGORITHM MATHEMATICA GENERATOR#
No test can prove definitively whether a nontrivial sequence (and the generator that produced it) is good enough as an RNG due to possible random or nonrandom local segments.The method illustrated in this Demonstration, known as the middle-square method, is a generalization of the first computer-based pseudorandom number generator (PRNG). These tests may be useful as a first step in determining whether or not a generator obviously fails or not as an RNG. If the compressed version of the sequence is short enough compared to the original size of the sequence given a threshold (defined by the tolerance control), the sequence is unlikely to be random.
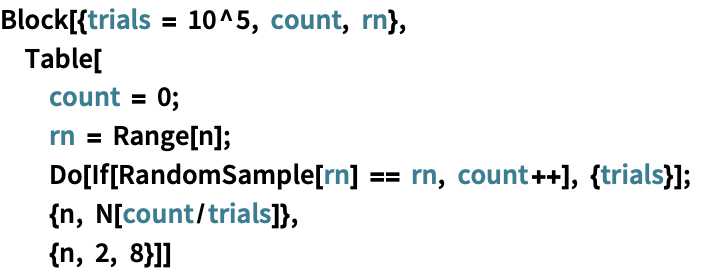
ate transformation (usually a compression algorithm) yields the desired random. Compression algorithms look for regularities. Pseudorandom number generators (or synonymously: deterministic random.

The compressibility test is based on algorithmic information theory. The oversimplified implementation of this test partitions the entire sequence into groups of 10 and then again into pairs, comparing each first segment with the second, looking for possible regularities. Autocorrelation is useful for finding repeating patterns, such as periodic sequences. It is the cross-correlation of the sequence with itself. The autocorrelation test looks for possible "hidden" functions producing the sequence. by applying a definite mathematical algorithm, starting from a particular seed.
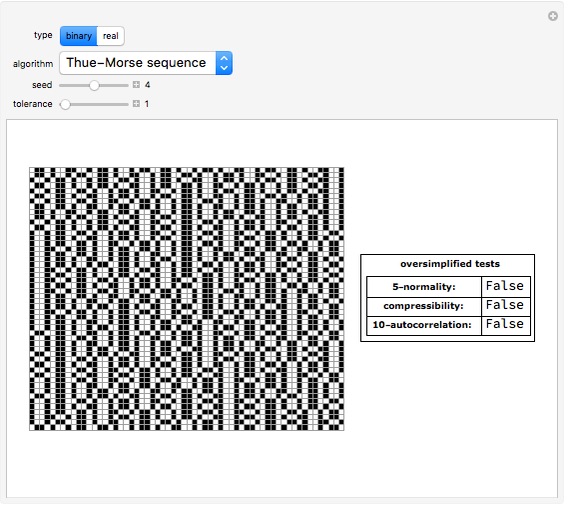
A normal sequence is a sequence whose digits show a uniform distribution, with all digits being equally likely the 5-normality test partitions the whole sequence into substrings of length 1 to 5 and tests each for whether the standard variation of their frequency differs by an acceptable value (the statistical tolerance). Some details about pseudorandom number generation in Mathematica. A random sequence is normal (but not the other way around). The oversimplified tests include two common statistical tests: normality and autocorrelation.


 0 kommentar(er)
0 kommentar(er)
